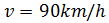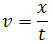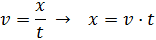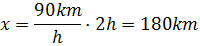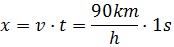concepto de
trayectoria y ecuación de posición
Cuando un
cuerpo se desplaza desde un punto a otro, lo hace describiendo una línea
geométrica en el espacio. A esa línea geométrica se le denomina trayectoria, y
está formada por las sucesivas posiciones del extremo del vector posición a lo
largo del tiempo. Es, por tanto, frecuente encontrar las coordenadas x, y y z
del vector de posición escritas en función del tiempo como x(t),y(t) y z(t)
para representar la evolución de la posición los cuerpos a lo largo del tiempo.
La
trayectoria de un cuerpo es la línea geométrica que un cuerpo describe en su
movimiento.
La ecuación
de posición o ecuación de trayectoria representa el vector de posición en
función del tiempo. Su expresión, en coordenadas cartesianas y en tres
dimensiones viene dada por:
r→(t)=x(t)i→+y(t)j→+z(t)k→
Donde:
r→(t) : es la
ecuación de posición o ecuación de trayectoria
x(t), y(t),
z(t): Son las coordenadas en función del tiempo.
i→,j→,k→ :Son
los vectores unitarios en las direcciones de los ejes OX, OY y OZ
respectivamente
En el caso de
aquellos problemas en los que sólo estés trabajando en dos dimensiones, puedes
simplificar las fórmulas anteriores eliminando la componente z. De esta manera,
la ecuación de posición en dos dimensiones queda r→(t)=x(t)i→+y(t)j→+z(t)k→
=x(t)i→+y(t)j→ . En la siguiente animación se ilustra el concepto de la
ecuación de posición o ecuación de trayectoria.
La
trayectoria es la línea geométrica que describen los cuerpos al moverse. En este
apartado vamos a estudiar:
Qué es la
ecuación de posición y su relación con la trayectoria
Los
principales tipos de ecuaciones de trayectoria que existen
Concepto de
trayectoria y ecuación de posición
Cuando un
cuerpo se desplaza desde un punto a otro, lo hace describiendo una línea
geométrica en el espacio. A esa línea geométrica se le denomina trayectoria, y
está formada por las sucesivas posiciones del extremo del vector posición a lo
largo del tiempo. Es, por tanto, frecuente encontrar las coordenadas x, y y z
del vector de posición escritas en función del tiempo como x(t),y(t) y z(t) para
representar la evolución de la posición los cuerpos a lo largo del tiempo.
La
trayectoria de un cuerpo es la línea geométrica que un cuerpo describe en su
movimiento.
La ecuación
de posición o ecuación de trayectoria representa el vector de posición en
función del tiempo. Su expresión, en coordenadas cartesianas y en tres
dimensiones viene dada por:
r→(t)=x(t)i→+y(t)j→+z(t)k→
Donde:
r→(t) : es la
ecuación de posición o ecuación de trayectoria
x(t), y(t),
z(t): Son las coordenadas en función del tiempo.
i→,j→,k→ :Son
los vectores unitarios en las direcciones de los ejes OX, OY y OZ
respectivamente
En el caso de
aquellos problemas en los que sólo estés trabajando en dos dimensiones, puedes
simplificar las fórmulas anteriores eliminando la componente z. De esta manera,
la ecuación de posición en dos dimensiones queda r→(t)=x(t)i→+y(t)j→+z(t)k→
=x(t)i→+y(t)j→ . En la siguiente animación se ilustra el concepto de la
ecuación de posición o ecuación de trayectoria.
Trayectoria
En la gráfica
se muestra la trayectoria (línea gris) que sigue un cuerpo representado por un
punto rojo a lo largo del tiempo. En nuestro ejemplo, esta trayectoria viene
dada por la ecuación de trayectoria r⃗(t) = (t+1)· i⃗ + (0.05 · t2 + 0.1 · t
+ 0.05)· j⃗
m, la cual define en cada instante de tiempo t cual es el vector de posición del cuerpo.
Arrastra el
deslizador que corresponde con el tiempo y comprueba como el cuerpo y su vector
de posición van cambiando a medida que lo mueves. El vector de posición en cada
instante de tiempo se obtiene al sustituir el valor de t que has elegido en la
ecuación de trayectoria.
Tipos de
ecuación de trayectoria
Además de la
expresión anterior, existen otras formas de expresar la trayectoria del
movimiento de un cuerpo. A continuación señalamos otros tipos de ecuaciones de
posición o ecuaciones de trayectoria:
Ecuaciones de
la trayectoria paramétricas: Se establece cada una de las coordenadas en
función del tiempo en la forma x=x(t), y=y(t), z=z(t). Por ejemplo, las
coordenadas paramétricas de un cuerpo que se desplaza en el plano x-y pueden
ser:
x=t+2
y=t2
Ecuación de
la trayectoria explícita: Se obtiene eliminando el parámetro t de las
expresiones anteriores y despejando una variable en función de la otra. En el
caso de nuestro ejemplo nos quedaría:
x=t+2 ⇒t=x−2
y=t2⇒y=(x−2)2
Ecuación de
trayectoria implícita: Se obtiene haciendo f(x,y)=0.
(x−2)2−y=0
Tomemos el
siguiente ejemplo, imagina que un tren se desplaza en dirección este a razón de
50 metros cada segundo. En el primer segundo el cuerpo se encuentra a 50 metros
del origen. En el segundo 2, el tren se encuentra a 100 m del origen y así
sucesivamente. Por tanto podríamos escribir:
La coordenada
x del movimiento en función del tiempo: x=50t m
Su ecuación
de posición: r→=50ti→ m
La distancia
al origen, dada por el módulo del vector de posición: ∣∣r→∣∣=5